Гипербола - это одна из четырех основных конических секций. В геометрии гипербола описывает кривую форму, которая отличается от эллипса тем, что у нее отсутствует центральная точка симметрии. График гиперболы состоит из двух ветвей, которые расходятся в бесконечности.
График гиперболы определяется уравнением вида y = k/x, где k - постоянное значение, а x и y - переменные значения. Это уравнение описывает горизонтальную или вертикальную гиперболу в зависимости от знаков коэффициентов k и x.
Область значений гиперболы зависит от ориентации графика. Для горизонтальных гипербол диапазон значения x может быть отрицательным или положительным, за исключением значения x = 0. А область значений y - отрицательная и положительная полуплоскости. Для вертикальных гипербол диапазон значений x - отрицательная и положительная полуплоскости, а область значений y может быть отрицательной или положительной, за исключением значения y = 0.
Пример гиперболы - гиперболический параболоид. Этот график представляет собой трехмерную гиперболу, которая может быть задана уравнением z = k/(x^2 - y^2). Он образуется путем вращения гиперболы вокруг одной из своих осей. Гиперболический параболоид широко используется в математике, физике и инженерии для моделирования различных явлений и объектов.
График гиперболы
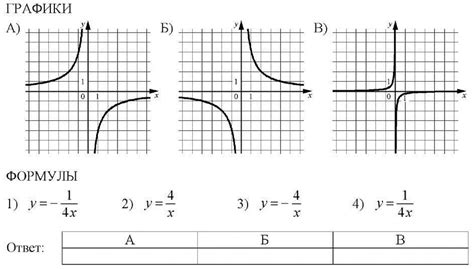
$$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$$
График гиперболы состоит из двух отделенных частей, которые называются ветвями гиперболы. Они симметричны относительно оси координат и не имеют общих точек. Вертикальные оси, которые проходят через центр гиперболы, называются асимптотами. График гиперболы приближается к асимптотам, но никогда их не пересекает.
Область значений гиперболы – это множество значений, которые могут принимать переменные x и y в уравнении гиперболы. Для гиперболы с уравнением $\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$, область значений x – все вещественные числа, а область значений y – все вещественные числа, кроме 0.
Гиперболы встречаются во многих областях математики и физики. Они широко используются в теории уравнений и анализе функций.
Примером графика гиперболы может служить график функции $y = \frac{1}{x}$. В этом случае оси координат являются асимптотами, и график функции стремится к ним, но никогда их не пересекает.
Определение и основные свойства

Основные свойства гиперболы:
| Название | Описание |
| Фокусы | У гиперболы всегда два фокуса, расположенных на оси симметрии кривой. |
| Оси | Гипербола имеет две оси симметрии, вертикальную и горизонтальную, пересекающуюся в её центре. |
| Фокусное расстояние | Разность между расстояниями от любой точки гиперболы до двух фокусов всегда равна постоянному значению. |
| Асимптоты | Гипербола имеет две асимптоты, которые являются прямыми линиями, стремящимися к границам кривой и пересекающимися в её центре. |
Гипербола может быть описана уравнением вида:
(x - h)2 / a2 - (y - k)2 / b2 = 1, где (h, k) - координаты центра гиперболы, a и b - полуоси.
Область значений гиперболы зависит от её ориентации и полуосей. Она может быть ограничена сверху или снизу только в зависимости от значений полуосей. Изображая график гиперболы на координатной плоскости, можно определить её область значений.
Уравнение гиперболы
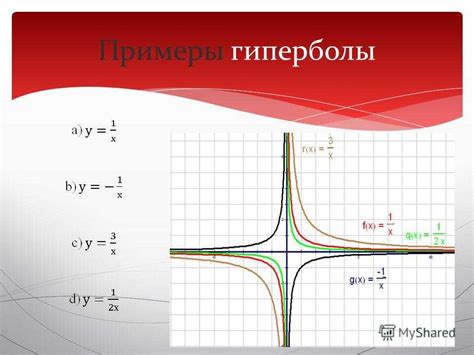
Общий вид уравнения гиперболы можно записать в виде:
- для гиперболы с центром в начале координат (0, 0): x2/a2 - y2/b2 = 1
- для гиперболы с центром в точке (h, k): (x-h)2/a2 - (y-k)2/b2 = 1
В уравнении гиперболы параметры a и b отвечают за форму гиперболы и называются полуосями гиперболы. Они определяют расстояния от центра гиперболы до вершин и фокусов.
Гипербола имеет две ветви, симметричные относительно центра гиперболы или оси гиперболы. Она также имеет две асимптоты, которые приближаются к ветвям гиперболы, но никогда не пересекают их.
Асимптоты гиперболы
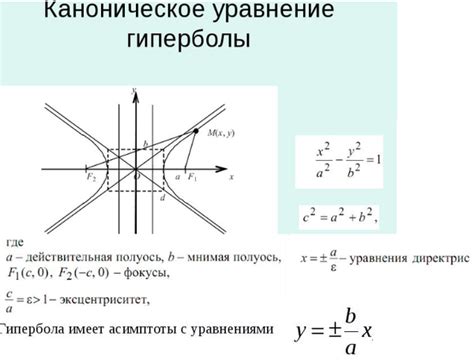 вида
вида y = a/x или x = b/y, где a и b - некоторые постоянные числа. В графике гиперболы присутствуют две специальные прямые - асимптоты.Асимптоты гиперболы являются вертикальной и горизонтальной прямыми, которые приводят график к бесконечности, но никогда не пересекают его.
Вертикальная асимптота гиперболы проходит через точку (0,0) и имеет уравнение вида x = 0. Она делит график на две половины: одну с положительными значениями функции, другую - с отрицательными.
Горизонтальная асимптота гиперболы имеет уравнение вида y = 0 и проходит также через точку (0,0). Она также делит график на две половины: одну с положительными значениями функции, другую - с отрицательными.
Асимптоты гиперболы помогают определить ее область значений и форму графика. Они представляют собой важные инструменты для анализа гиперболических функций и решения математических задач.
Центр и фокусы гиперболы
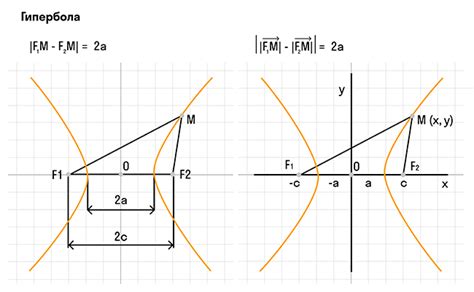
Центр гиперболы - это точка, которая находится посередине между двумя фокусами и на оси симметрии. В уравнении гиперболы, центр обозначается как (h, k), где h - координата по оси абсцисс, а k - координата по оси ординат.
Фокусы гиперболы - это точки, которые находятся внутри гиперболы, симметрично расположенные относительно центра. Расстояние от центра гиперболы до каждого из фокусов обозначается буквой с - это фокусное расстояние. Фокусное расстояние связано с уравнением гиперболы и задается следующей формулой: с^2 = a^2 + b^2, где a - половина длины большой оси гиперболы, а b - половина длины малой оси гиперболы.
Центр и фокусы гиперболы играют важную роль в графическом представлении и анализе гиперболы. Уравнение гиперболы может быть записано в виде (x - h)^2/a^2 - (y - k)^2/b^2 = 1 (для гиперболы с горизонтальными осями) или (y - k)^2/b^2 - (x - h)^2/a^2 = 1 (для гиперболы с вертикальными осями) с использованием центра и фокусного расстояния.
Например, рассмотрим гиперболу с центром в точке (0, 0) и фокусным расстоянием c = 5. Тогда уравнение гиперболы с горизонтальными осями будет иметь вид x^2/16 - y^2/9 = 1, где a = 4 и b = 3. График этой гиперболы будет представлять из себя две ветви, симметрично расположенные относительно осей x и y, проходящие через фокусы и центр гиперболы.
Параметрическое представление гиперболы
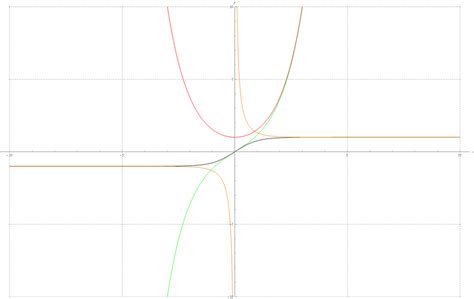
Гиперболу можно представить в виде параметрических уравнений, которые описывают движение точки на кривой. Параметрическое представление гиперболы позволяет наглядно изображать график и исследовать основные свойства этой фигуры.
Параметрические уравнения гиперболы имеют вид:
- x = a * sec(t) + h
- y = b * tan(t) + k
где a и b - полуоси гиперболы, h и k - координаты центра гиперболы, а t - параметр, который пробегает всевозможные значения от 0 до 2π (циклически).
На графике гиперболы каждой точке соответствует определенное значение параметра t. Перебирая значения t вместе соответствующие значения x и y, можно построить график гиперболы.
Параметрическое представление гиперболы позволяет удобно находить точки пересечения гиперболы с другими кривыми, проводить касательные, определять фокусы и другие положения фигуры.
Например, если a=2, b=3, h=0, k=0, то параметрические уравнения гиперболы будут иметь вид:
- x = 2 * sec(t)
- y = 3 * tan(t)
Такое представление гиперболы помогает увидеть график и дает возможность легко находить координаты точек на гиперболе.
Область значений гиперболы

Для гиперболы с центром в начале координат (0, 0) и уравнением вида y = a/x, где a – положительная константа, область значений будет состоять из всех действительных чисел, кроме 0.
Для гиперболы с центром в точке (h, k) и уравнением вида (x-h)^2/a^2 - (y-k)^2/b^2 = 1, где a и b – положительные константы, областью значений будет являться отрезок (–∞, k-b) объединенный с отрезком (k+b, ∞) на оси y.
Таким образом, область значений гиперболы может быть ограничена или неограниченной, в зависимости от ее уравнения и параметров. Она может включать или исключать определенные значения на оси x и оси y.
Примеры гиперболических функций
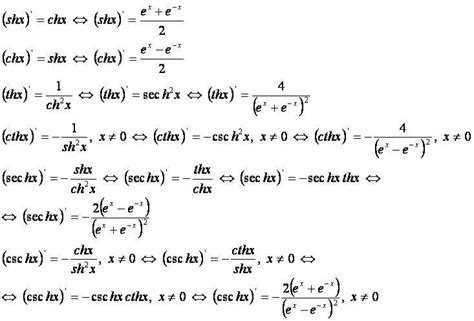
Гиперболические функции представляют собой особую группу математических функций, которые связаны с гиперболическими тригонометрическими функциями. Вот несколько примеров гиперболических функций:
1. Гиперболический синус (sinh):
Гиперболический синус функции sinh(x) определяется как полусумма экспоненты и обратной экспоненты от аргумента x. График функции имеет форму подобную параболе.
Пример:
sinh(x) = (e^x - e^(-x)) / 2
2. Гиперболический косинус (cosh):
Гиперболический косинус функции cosh(x) определяется как полусумма экспоненты и обратной экспоненты от аргумента x. График функции имеет форму подобную параболе, но отраженную относительно оси y.
Пример:
cosh(x) = (e^x + e^(-x)) / 2
3. Гиперболический тангенс (tanh):
Гиперболический тангенс функции tanh(x) определяется как частное гиперболического синуса и гиперболического косинуса функций sinh(x) и cosh(x). График функции имеет форму подобную гиперболе.
Пример:
tanh(x) = sinh(x) / cosh(x)
Это лишь некоторые из гиперболических функций, которые находят применение в различных областях науки и техники. Они обладают своими характерными свойствами и используются для решения задач, связанных с моделированием и анализом систем.
Связь гиперболы с другими математическими понятиями

| Понятие | Связь с гиперболой |
|---|---|
| Эллипс | Гипербола и эллипс - это две разные конические секции. Оба являются кривыми второго порядка, но у эллипса эксцентриситет меньше единицы, в то время как у гиперболы эксцентриситет больше единицы. Эллипс можно рассматривать как усеченную гиперболу. |
| Парабола | Гипербола и парабола - это два разных типа кривых второго порядка. Обе они имеют фокусы, но у параболы фокус и директриса находятся на бесконечности, в то время как у гиперболы они располагаются на конечном расстоянии друг от друга. |
| Асимптота | У гиперболы есть две асимптоты, которые представляют из себя прямые линии, к которым гипербола стремится бесконечно близко по мере ее расширения. Асимптоты могут использоваться для построения графика гиперболы и определения ее области значений. |
| Фокус | Фокусы гиперболы - это две точки, сумма расстояний от которых до любой точки гиперболы постоянна. Фокусы являются важными элементами гиперболы и определяют ее форму и параметры. |
| Директриса | Директриса гиперболы - это прямая линия, относительно которой гипербола симметрична. Расстояние от любой точки гиперболы до директрисы равно модулю разности расстояний от этой точки до фокусов гиперболы. |
Это лишь некоторые из связей гиперболы с другими математическими понятиями. Гипербола является важной и интересной кривой в математике и находит применение в различных областях, таких как физика, инженерия и экономика.